“无字证明”是什么？从三维视角看二维问题，有趣的现象发生了

1989年，在《美国数学月刊》上出现了一个非常有趣的数学问题——可利颂镶嵌定理。

可利颂糖果

“可利颂”是法国的一种传统糖果，外形跟杏仁很像。我们可以让它的边缘锋利起来，也就变成了一个菱形。

如果这个菱形恰巧由两个边长为1的等边三角形组成，那么拿来一个边长为n的正六边形盒子，并将糖果一个个地紧贴着平放进去，会发生什么呢？

有趣的“可利颂问题”

首先，我们要明确一下糖果的摆放方式，它可以水平放置，也可以向左倾斜，或者向右倾斜。

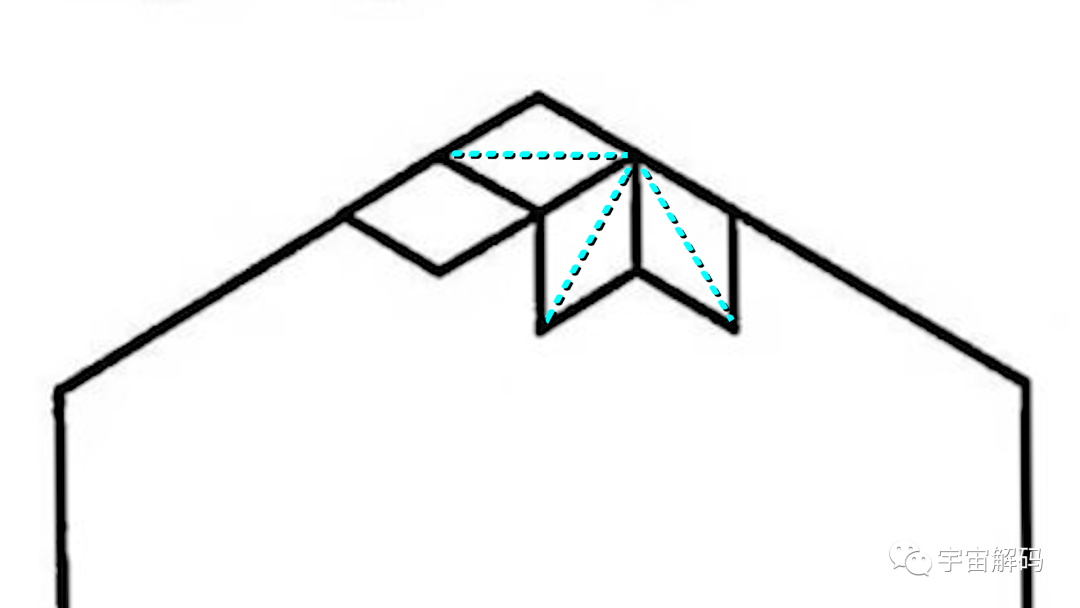
在填充完毕后，你会发现：不论具体位置怎样摆放，每个固定朝向的糖果数量总是盒子中糖果总数的三分之一。这是什么原因呢？

每种方向的糖果数量刚好是总量的三分之一

在文章的最后，作者提供了一个非常帅气的“证明”方式——给菱形涂上颜色。

即，水平摆放的菱形是蓝色的，向左倾斜的菱形是黄色的，向右倾斜的菱形是红色的。

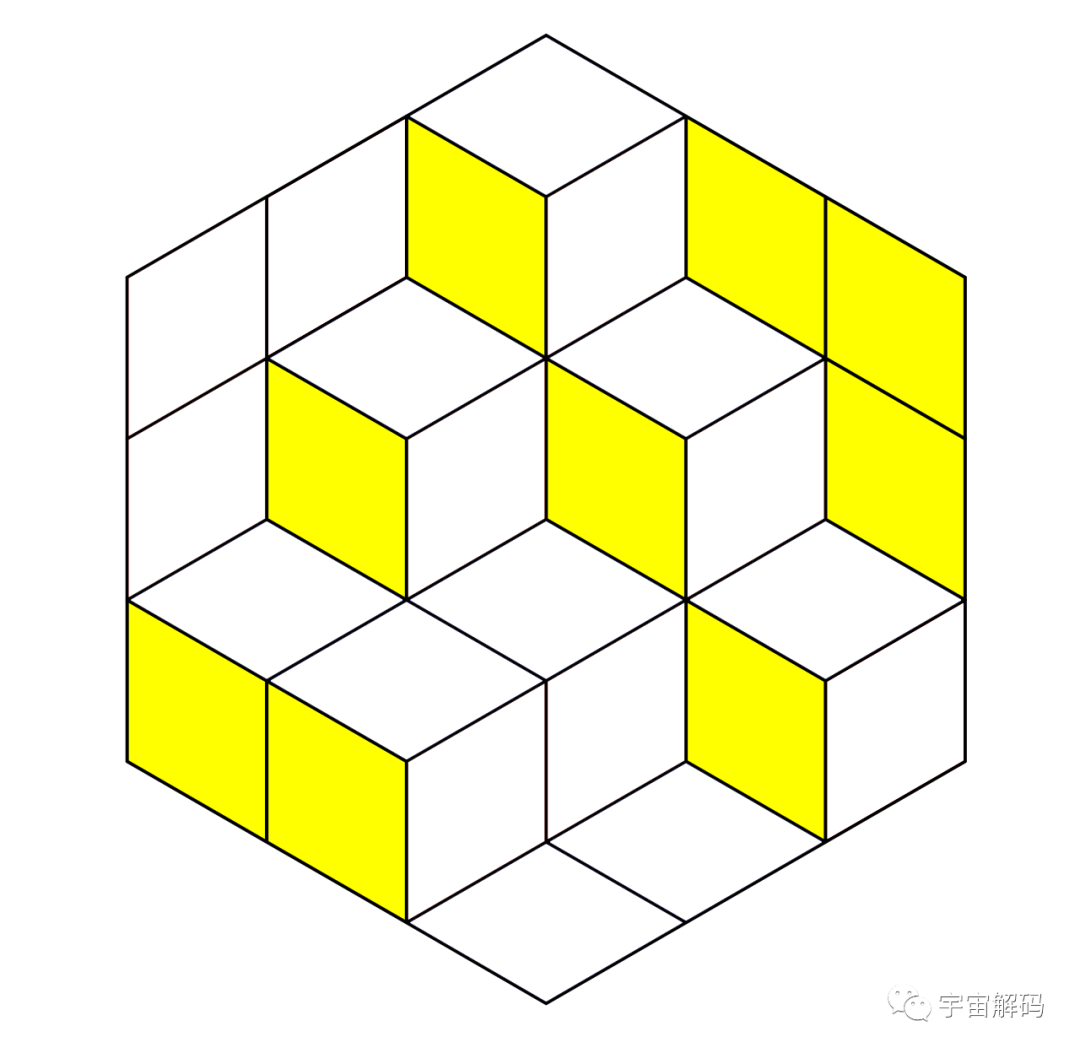
如此一来，整个正六边形瞬间变成了一个三维立体图形。我们可以从不同视角观察，这时你会惊讶地发现：它的正视图刚好是一个黄色的大正方形，侧视图是一个红色的大正方形，俯视图则是一个蓝色的大正方形。并且，它们都由n的平方个小正方形组成。也就是说，在摆放可利颂时，用到的不同朝向的菱形数量是相等的，都是总数的三分之一。

在刚刚的“证明”过程中，虽然没有用到数字和公式，但却把一个纯组合数学问题和立体空间图形完美地结合到了一起，让人拍案叫绝！而“可利颂镶嵌定理”也就此成为一道经典的“无字证明”题。2003年出版的《最迷人的数学趣题——一位数学名家精彩的趣题珍集》还用它做了封面。

当然，类似的“暴力证明”还有很多，比如我们最最熟悉的勾股定理。

首先，找来四个完全一样的直角三角形卡片，它们的短直角边为a，长直角边为b，斜边为c。

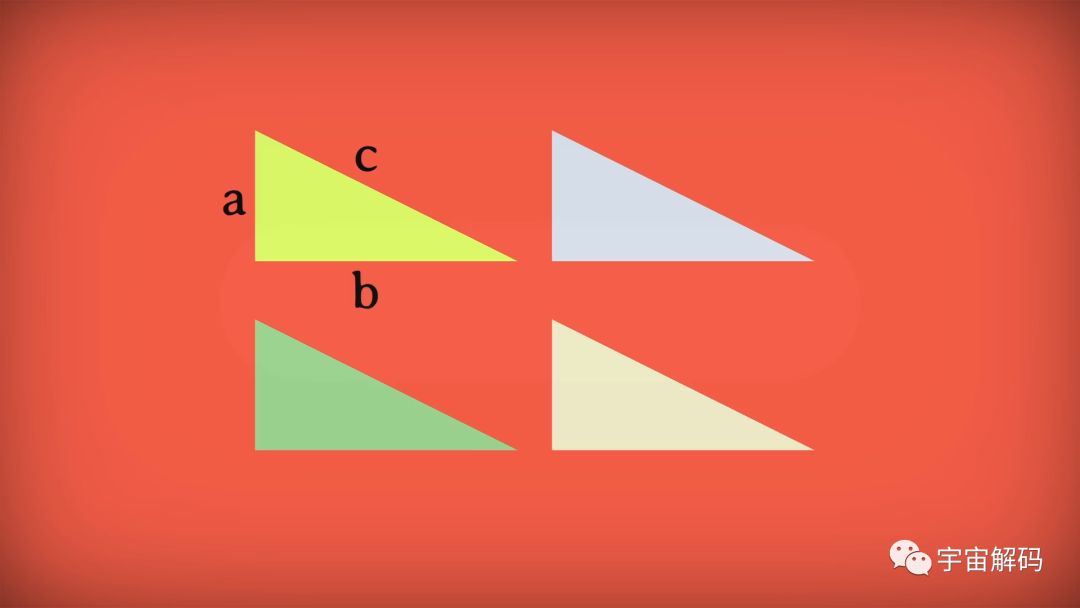
然后，将其拼成一个大正方形，中间空出来的部分也是一个正方形，它的面积为c方。

接下来，保持整体形状不变，调整一下三角形的摆放方式，此时空出来的位置刚好是一大一小两个正方形，并且它们的面积就是b方和a方。

除此之外，你还可以制作一个模型。中间是一个直角三角形，分别以它的三条边为边长向外做正方形容器。最开始，下方两个容器里的水是满的，在转动转盘后，只听水哗啦啦地流向大正方形，最后刚刚好盛得满满当当的。

声明：部分图文来源于网络，版权归原作者所有，侵权请联系删除：wzwt58@qq.com。本站发布此信息目的在于传播更多信息，与本网站立场无关，不保证该信息（包括但不限于文字、数据及图表）准确性、真实性、完整性等。本文地址：https://www.quqiwen.com/kxts/25110.html